Note: This post represents the synthesis of the thoughts, procedures and experiences of others as represented in the articles read in advance (see previous posts) and the discussion among the students and instructor during the Advanced Analytic Techniques class at Mercyhurst University in October 2015 regarding Bayesian Analysis as an Analytic Technique specifically. This technique was evaluated based on its overall validity, simplicity, flexibility and its ability to effectively use unstructured data.
Description:
Bayesian Analysis is an statistical analytic method based on a mathematical theorem used to determine the probability of an event. The core of Bayesian Analysis is the use of updated knowledge as the analyst learns more information. As evidence is gathered, the more nuanced the estimate will get. As the process goes along, a higher accuracy of a probabilistic prediction will be produced.
Strengths:
- Method gives a quantitative result to analysis.
- By applying Bayes an analyst evaluates/weighs the new evidence and finds a revised probability by considering the previous one(s).
- Method is a very structured technique that is easily replicated.
- Method can provide a numerical value for words of estimative probability.
- Method prevents vividness and recentness biases.
Weaknesses:
- Can be manipulated by cognitive biases because it relies on subjective thinking.
- Since this method requires the analysts to convert living events into the numbers, it may require some expertise/background to some extent in order to get meaningful results. However, this may not be called as the weakness, rather it could be a challenge for analysts.
- The math can scare people away from learning this technique.
- Decision-makers at a tactical level may not understand this technique.
- There is a time factor which can limit the practicality of using Bayes in some situations.
- It is very hard to determine the importance of a piece of evidence before something happens.
How-To:
While there are many different applications of Bayes, the basic formula is A=BxC or “the probability of an underlying cause (hypothesis) equals its previous probability multiplied by the probability of the observed event was caused by that hypothesis.” Since the exact probabilities are impossible to evaluate, estimated probabilities can be generated by using historical evidence or expert opinion to answer those complex questions.
The Bayesian formula is as follows:
Personal Application of Technique:
This methodology was applied through a scenario similar to the board game “Battleship.” In the scenario, which can be found in the “Bayesian Battleship” Powerpoint below, the class was an analyst for the Air Force in direct communication with a fighter pilot who is approaching a naval battle what has been divided into two sectors, the Lower-Right Quadrant (LRQ, 25 total squares, 25 empty), and the Rest of Board (RoB, 75 total squares, 51 empty). The analyst’s mission was to destroy the enemy submarine; however, we do not know where the enemy submarine is.
The problem was broken up into four parts representing added information to take into account. The first part is determining the probability that the enemy submarine is in the LRQ based on information that there is a 50-50 chance his sub is in either. The second part builds on the first, adding that the enemy submarine is about to fire on one of the allied ships, but the enemy submarine must be in a certain firing position (perpendicular to and centered on the enemy ship) which decreases the overall available locations of the enemy submarine.
The third part introduces the presence of an allied stealth submarine on the board, but we do not know where the allied submarine is, and it does not have any communications capabilities. Based on a recent sighting, there is a 90% chance that the allied submarine is in the LRQ. The problem is to find what is the probability that the allied submarine in the LRQ.
Finally, in the fourth part the pilot has an emergency where his missiles lock up and his aircraft is going down. Therefore, we must determine to which sector the pilot should set his autopilot, taking into account the main goal of destroying the enemy submarine and not hitting the allied submarine. The greatest likelihood is that the aircraft will hit the water and not hit either of the ships. The results are that in the LRQ, the aircraft has probabilities of 9.4% to hit the enemy submarine, 13% to hit the allied submarine, and 77.6% to hit the water. In the RoB sector, the aircraft has probabilities of 8.7% to hit the enemy submarine, 0.34% to hit the allied submarine, and 91% to hit the water. Based on these probabilities, the pilot should set his autopilot to the RoB sector because there is a significantly lower probability of hitting the allied submarine while only a slightly lower probability of hitting the enemy submarine. In either sector, the greatest probability is that the aircraft will hit the water.
For additional information:
Bayes Theorem and Intelligence
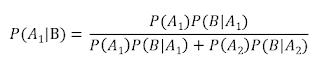



No comments:
Post a Comment